Path Queries
This page discusses Path Queries in Stardog - a feature to find paths between nodes in an RDF graph.
Page Contents
Overview
Stardog extends SPARQL to find paths between nodes in the RDF graph, which we call path queries. They are similar to property paths, which traverse an RDF graph and find pairs of nodes connected via a complex path of edges. However, SPARQL property paths only return the start and end nodes of a path and do not allow variables in property path expressions. Stardog path queries return all intermediate nodes on each path – that is, they return a path from start to end – and allow arbitrary SPARQL graph patterns to be used in the query.
Read A Path of Our Own, and GraphQL and Paths to learn more about path queries.
Path Query Syntax
We add path queries as a new top-level query form. In other words, it is separate from SELECT, CONSTRUCT or other query types. The syntax is as follows:
The graph pattern in the VIA clause must bind both ?s and ?e variables.
Next, we present informal examples of common path queries. We will conclude with formal Path Query Evaluation Semantics.
Shortest Paths
Suppose we have a simple social network where people are connected via different relationships:
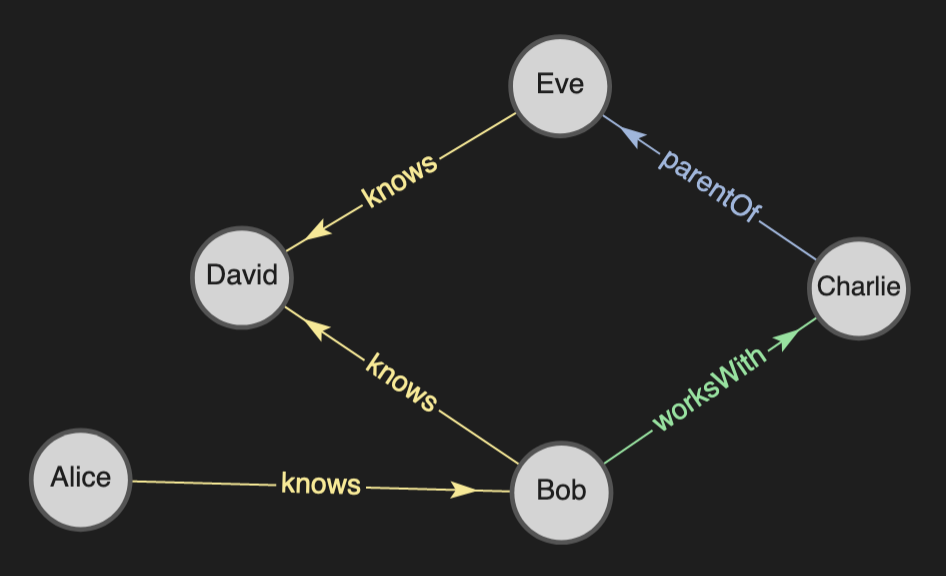
If we want to find all the people Alice is connected to and how she is connected to them, we can use the following path query:
We specify a start node for the path query, but the end node is unrestricted. All paths starting from Alice will be returned. Note that we use the shortcut VIA ?p instead of a graph pattern to match each edge in the path. This is a syntactic sugar for VIA { ?s ?p ?e }. Similarly we could use a predicate, e.g. VIA :knows or a property path expression, e.g. VIA :knows | :worksWith.
This query is effectively equivalent to the SPARQL property path :Alice :knows+ ?y, but the results will include the nodes in the path(s). The path query results are printed in a tabular format by default:
Each row of the result table shows one edge, and adjacent edges on a path are printed on subsequent rows of the table. Multiple paths in the results are separated by an empty row. We can change the output format to text, which serializes the results in a property graph-like syntax:
Execution happens by recursively evaluating the graph pattern in the query and replacing the start variable with the binding of the end variable in the previous execution. If the query specifies a start node, that value is used for the first evaluation of the graph pattern. If the query specifies an end node (which our example doesn’t), execution stops when we reach the end node. Only simple cycles, i.e. paths where the start and end nodes coincide, are allowed in the results.
The Stardog optimizer may choose to traverse paths backwards, i.e. from the end node to the start, for performance reasons, but it does not affect the results.
We can specify the end node in the query and restrict the kind of patterns in paths to a specific property, as in the next example. It queries how Alice is connected to David via knows relationships:
This query would return a single path with two edges:
Complex Paths
Graph patterns inside the path queries can be arbitrarily complex. Suppose we want to find undirected paths between Alice and David in this graph. Then we can make the graph pattern to match both outgoing and incoming edges:
Sometimes a relationship between two nodes might be implicit. In other words, there might not be an explicit link between those two nodes in the RDF graph. Consider the following set of triples that show some movies and actors who starred in those movies:
There is an implicit relationship between actors based on the movies they appeared together. We can use a basic graph pattern with multiple triple patterns in the path query to extract this information:
This query executed against the above set of triples would return three paths:
If the movie is irrelevant, then a more concise version can be used:
All Paths
Path queries return only shortest paths by default. We can use the ALL keyword in the query to retrieve all paths between two nodes. For example, the query above returned only one path between Alice and David. We can get all paths as follows:
The ALL qualifier can dramatically increase the number of paths, so use with caution.
Cyclic Paths
There’s a keyword CYCLIC to query specifically for cyclic paths in the data. For example, there might be a dependsOn relationship in the database, and we might want to query for cyclic dependencies:
Again, arbitrary cycles in the paths are not allowed to ensure a finite number of results.
Limiting Paths
In a highly connected graph, the number of possible paths between two nodes can be impractically high. There are two different ways we can limit the number of results of path queries. The first possibility is to use the LIMIT keyword, just like in other query types. We can ask for at most 2 paths starting from Alice as follows:
This query would return 2 results, as expected :
Note that the path from Alice to Charlie is not included in this result even though it is not any longer than the path between Alice and David. This is because with LIMIT the query will stop producing results as soon as the maximum number of paths are returned.
The other alternative for limiting the results is by specifying the maximum length of paths that can be returned. The following query shows how to query for paths that are at most 2 edges long:
This time we will get 3 results:
It is possible to use both the LIMIT and MAX LENGTH keywords in a single query.
Path Queries With Start and End Patterns
In all examples presented so far, the start and end variables were either free variables or bound to a single IRI. This is insufficient for navigating paths which must begin at multiple nodes satisfying certain conditions and terminate at nodes satisfying some other conditions. Assume the movie and actor data above is extended with information about the date of birth of each actor:
Now, having only variables and constants as valid path start and end expressions would make it hard to write a query to find all connections between Kevin Bacon and actors over 80 years old. The following attempt, for example, won’t match any data:
The problem is that the age filter is applied at each recursive step, i.e. the query is looking for paths where every intermediate actor is over 80, but none of those co-starred with Kevin Bacon (in our toy dataset). Instead we need a query which checks the condition only at candidate end nodes:
This query will return the expected results, along with the date of birth for end nodes:
The shortest path semantics applies to each pair of start and end nodes independently. This means that for nodes :A and :B, only the shortest paths from :A to :B will be returned. However, when the query uses start or end patterns, it may return paths of different lengths for different start or end nodes. For example, a path from :A to :B may be longer in the results than a path from :A to :C. This has implications for performance since the engine cannot avoid exploring paths which are longer than those already found because they may end at a different node. We recommend using the MAX LENGTH keyword in path queries with start or end patterns.
Path Queries With Reasoning
As other kinds of queries, path queries can be evaluated with reasoning. If reasoning is enabled, a path query will return paths in the inferred graph. In other words, each edge corresponds to a relationship between the nodes which is inferred from the data based on the schema.
Consider the following example:
Adding the following rule (or an equivalent OWL sub-property chain axiom) infers :partOf edges based on compositions of :partOf and :locatedIn edges:
Now the following path query will find the inferred path from :Arlington to :NorthAmerica via :DCArea and :US:
This feature should be used with care. There may be far more paths than one expects. Also keep in mind that some patterns are particularly expensive with reasoning, e.g. triple patterns with the predicate variable unbound or with a variable in the path.
Path Query Evaluation Semantics
Given a pair of variable names s and e, a path is a sequence of SPARQL solutions S[1], ..., S[n] s.t. S[i](t) = S[i-1](s) for i from 2 to n. We call the S[0](s) and S[n](t) values the start and end nodes of the path, respectively. Each solution in the sequence is called an edge.
The evaluation semantics of path queries is based on the following recursive extension of the SPARQL solution:
Informally, such extensions allow us to represent each path as a single solution, where a distinguished variable (in the sequence called a path variable) is mapped to an ordered array of solutions representing edges.
We first consider simple path queries for ALL paths with only variables after the START and END keywords, i.e. queries of the form PQ(s, e, p, P), where s and e are start and end variable names, p is a path variable name, and P is a SPARQL graph pattern. Given a dataset D with the active graph G, abbreviated as D(G), we define eval(PQ(s, e, P), D(G)) as a set of all such (extended) solutions S that:
where sub(P, var, t) is a graph pattern obtained by substituting the variable var by the fixed RDF term t.
Informally, conditions (2) and (3) state that each edge in a path is obtained by evaluating the path pattern with the start variable substituted by the end variable value of the previous edge (to ensure connectedness). The conditions (4) and (5) bind the s and e variables in the top level solution.
Next we define the semantics of path queries with start and end patterns:
where PS and PE are start and end graph patterns which must bind s and e variables, respectively. Here Join stands for the standard SPARQL join semantics, which does not require extensions. This is because joins are performed on variables s and e, which bind to RDF terms only, rather than arrays or solutions (conditions (4) and (5) above ensure that).
Finally, we note that path queries with start or end constants are a special case of path queries with the corresponding singleton VALUES patterns, e.g.:
is syntactic sugar for:
Keywords SHORTEST (default) and CYCLIC are self-explanatory and place further restrictions on each S(p): the sequence should be the shortest among all results or represent a simple cycle. The solution modifiers LIMIT and OFFSET have the exact same semantics as in SPARQL 1.1.