Reasoning & Inference
This chapter discusses what Stardog’s reasoning capabilities are and how to use them. This page provides an overview of the reasoning capabilities. See the Chapter Contents for what else is included in this chapter.
Page Contents
Overview
In this chapter we describe how to use Stardog’s reasoning capabilities; we address some common problems and known issues. We also describe Stardog’s approach to query answering with reasoning in some detail, as well as a set of guidelines that contribute to efficient query answering with reasoning. If you are not familiar with the terminology, you can peruse the section on terminology.
The semantics of Stardog’s reasoning is based in part on the OWL 2 Direct Semantics Entailment Regime. However, the implementation of Stardog’s reasoning system is worth understanding as well. For the most part, Stardog performs reasoning in a lazy and late-binding fashion: it does not materialize inferences; but, rather, reasoning is performed at query time according to a user-specified “reasoning type”. This approach allows for maximum flexibility while maintaining excellent performance; you only pay for the reasoning that you use; no more and no less. Eager materialization is mostly a great strategy for hard disk manufacturers. The one exception to this general approach is equality reasoning which is eagerly materialized. See Same As Reasoning below for more information.
Reasoning Types
Reasoning can be enabled or disabled using a simple boolean flag in HTTP (see the HTTP Docs); the CLI with -r or --reasoning in the query execute command and in the Java APIs as a query option/parameter. We describe this in more detail in the Using Reasoning section below.
When reasoning is set to:
false: No axioms or rules are considered; no reasoning is performed.true: Axioms and rules are considered and reasoning is performed according to the value of thereasoning.typedatabase option.
Reasoning is disabled by default; that is, no reasoning is performed without explicitly setting the reasoning flag to true.
When reasoning is enabled by the boolean flag, the axioms and rules in the database are first filtered according to the value of the reasoning.type database option. The default value of reasoning.type is SL and for the most part users don’t need to worry too much about which reasoning type is necessary since SL covers all of the OWL 2 profiles as well as user-defined rules via SWRL. However, this value may be set to any other reasoning type that Stardog supports:
RDFSis the OWL 2 axioms allowed in RDF Schema, main subclasses, subproperties, domain and rangeQLfor the OWL2 QL axiomsRLfor the OWL2 RL AxiomsELfor the OWL2 EL axiomsDLfor the OWL2 DL axiomsSLfor a combination ofRDFS,QL,RL, andELaxioms, plus SWRL rules. Any axiom outside the selected type will be ignored by the reasoner.
The DL reasoning type behaves significantly different than other types. Stardog normally uses the Query Rewriting technique for reasoning which scales very well with increasing number of instances; only the schema needs to be kept in memory. But query rewriting cannot handle axioms outside the OWL 2 profiles; however, DL reasoning type can be used so that no axiom or rule is ignored as long as they satisfy the OWL 2 DL restrictions. With DL reasoning, both the schema and the instance data need to pulled into memory, which limits its applicability with large number of instances. DL reasoning also requires the database to be logically consistent or no reasoning can be performed. Finally, DL reasoning requires more computation upfront compared to query rewriting which exhibits a “pay-as-you-go” behavior.
DL reasoning is not something that we recommend using due to scalability issues. It may be deprecated and removed in a future version of Stardog.
The reasoning.type can also be set to the special value NONE which will filter all axioms and rules thus effectively disables reasoning. This value can be used for the database option to prevent reasoning to be used by any client even though they might enable it with the boolean flag on the client side.
Using Reasoning
In order to perform query evaluation with reasoning, Stardog requires a schema, sometimes called a “data model”, “ontology”, or “TBox”, to be present in the database. Since schemas are serialized as RDF, they are loaded into a Stardog database in the same way that any RDF is loaded into a Stardog database. Also, note that, since the schema is just more RDF triples, it may change as needed: it is neither fixed nor compiled in any special way.
The schema may reside in the default graph, in a specific named graph, or in a collection of graphs. You can tell Stardog where the schema is by setting the reasoning.schema.graphs database configuration option to one or more named graph URIs.
If you want the default graph to be considered part of the schema, then you can use the special built-in URI tag:stardog:api:context:default.
If you want to use all local (non-virtual) named graphs (that is, to tell Stardog to look for the schema in every local named graph), you can use tag:stardog:api:context:local. This is the default value for reasoning.schema.graphs.
This design is intended to support both of Stardog’s primary use cases:
- managing the data that constitutes the schema
- reasoning with the schema during query evaluation
Query Answering
All of Stardog’s interfaces (API, network, and CLI) support reasoning during query evaluation. All types of queries (that is, SELECT, ASK, CONSTRUCT, PATHS, DESCRIBE, and updates can be evaluated with reasoning. When reasoning is enabled, it applies to all query patterns in WHERE and VIA blocks.
It is possible to selectively disable it for certain parts of the query using the #pragma reasoning hint. See Reasoning Query Hints
CLI
In order to evaluate queries in Stardog using reasoning via the command line, we use the --reasoning flag in the query execute command:
$ stardog query execute --reasoning myDB "SELECT ?s { ?s a :Pet } LIMIT 10"
HTTP
For HTTP, the reasoning flag is specified either with the other HTTP request parameters:
$ curl -u admin:admin -X GET "http://localhost:5820/myDB/query?reasoning=true&query=..."
or, as a segment in the URL:
$ curl -u admin:admin -X GET "http://localhost:5820/myDB/query/reasoning?query=..."
See the HTTP API for a detailed look at the API to perform a SPARQL query with reasoning enabled.
Programmatically
See the chapter on Programming for the details of how to use reasoning from the various programming languages Stardog supports.
Reasoning with Multiple Schemas
There is a default schema associated with each database whose content is controlled by the reasoning.schema.graphs database configuration option as explained above. However, there are certain use cases where one might need to use different schemas to answer different queries. Some example use cases are as follows:
- There are two different versions of a schema that evolved over time and older legacy applications need to use the previous version of the schema whereas the newer applications need to use the newer version.
- Different applications require different rules and business logic, e.g. threshold for a concept like
LoworHighmight change based on the context. - There could be a very large number of axioms and rules in the domain that can be partitioned into smaller schema subsets for performance reasons.
Starting with version 7.0, Stardog supports schema multi-tenancy: reasoning with multiple schemas and specifying a schema to be used for answering a query. Each schema has a name and a set of named graphs and when the schema is selected for answering a query the axioms and rules stored in the associated graphs will be taken into account. A named schema can be selected for a query using the --schema parameter in the query execute command:
$ stardog query execute --schema petSchema myDB "SELECT ?s { ?s a :Pet } LIMIT 10"
When the --schema parameter is used the --reasoning parameter does not need to be specified and will have no effect. But using --reasoning flag without a --schema parameter is equivalent to specifying --schema default.
The named schemas are defined via the reasoning.schemas configuration option that is a set of schema name and graph IRI pairs. There is convenience functionality provided in the CLI and Java API to manage schemas. The named graphs for a new or an existing schema can be set as follows using stored namespaces or full IRIs:
$ stardog reasoning schema --add dogSchema --graphs :dogGraph :petGraph -- myDB
The schemas can be removed using the reasoning schema command with the --remove flag. The --list option will list all the defined schemas and their named graphs:
$ stardog reasoning schema --list myDB
+-----------+---------------------------------+
| Schema | Graphs |
+-----------+---------------------------------+
| default | <tag:stardog:api:context:local> |
| catSchema | :petGraph, :catGraph |
| dogSchema | :petGraph, :dogGraph |
| petSchema | :petGraph |
+-----------+---------------------------------+
Explaining Reasoning Results
Stardog can be used to check if the current database logically entails a set of triples; moreover, Stardog can explain why this is so. An explanation of an inference is the minimum set of statements explicitly stored in the database that, together with the schema and any valid inferences, logically justify the inference. Explanations are useful for understanding data, schema, and their interactions, especially when large number of statements interact with each other to infer new statements.
Explanations can be retrieved using the CLI reasoning explain command by providing an input file that contains the inferences to be explained:
$ stardog reasoning explain myDB inference_to_explain.ttl
The output is displayed in a concise syntax designed to be legible; but it can be rendered in any one of the supported RDF syntaxes if desired. Explanations are also accessible through the HTTP API and programmatically. See the example in the stardog-examples Github repo for more details about retrieving explanations programmatically.
Proof Trees
Proof trees are a hierarchical presentation of multiple explanations (of inferences) to make data, schemas, and rules more intelligible. Proof trees provide an explanation for an inference or an inconsistency as a hierarchical structure. Nodes in the proof tree may represent an assertion in a Stardog database. Multiple assertion nodes are grouped under an inferred node.
Examples
For example, if we are explaining the inferred triple :Alice rdf:type :Employee, the root of the proof tree will show that inference:
INFERRED :Alice rdf:type :Employee
The children of an inferred node will provide more explanation for that inference:
INFERRED :Alice rdf:type :Employee
ASSERTED :Manager rdfs:subClassOf :Employee
INFERRED :Alice rdf:type :Manager
The fully expanded proof tree will show the asserted triples and axioms for every inference:
INFERRED :Alice rdf:type :Employee
ASSERTED :Manager rdfs:subClassOf :Employee
INFERRED :Alice rdf:type :Manager
ASSERTED :Alice :supervises :Bob
ASSERTED :supervises rdfs:domain :Manager
The CLI reasoning explain command prints the proof tree using indented text; but, using the Java API, it is easy to create a tree widget in a GUI to show the explanation tree, such that users can expand and collapse details in the explanation.
Another feature of proof trees is the ability to merge multiple explanations into a single proof tree with multiple branches when explanations have common statements. Consider the following example database:
#schema
:Manager rdfs:subClassOf :Employee
:ProjectManager rdfs:subClassOf :Manager
:ProjectManager owl:equivalentClass (:manages some :Project)
:supervises rdfs:domain :Manager
:ResearchProject rdfs:subClassOf :Project
:projectID rdfs:domain :Project
#instance data
:Alice :supervises :Bob
:Alice :manages :ProjectX
:ProjectX a :ResearchProject
:ProjectX :projectID "123-45-6789"
In this database, there are three different unique explanations for the inference :Alice rdf:type :Employee:
Explanation 1
:Manager rdfs:subClassOf :Employee
:ProjectManager rdfs:subClassOf :Manager
:supervises rdfs:domain :Manager
:Alice :supervises :Bob
Explanation 2
:Manager rdfs:subClassOf :Employee
:ProjectManager rdfs:subClassOf :Manager
:ProjectManager owl:equivalentClass (:manages some :Project)
:ResearchProject rdfs:subClassOf :Project
:Alice :manages :ProjectX
:ProjectX a :ResearchProject
Explanation 3
:Manager rdfs:subClassOf :Employee
:ProjectManager rdfs:subClassOf :Manager
:ProjectManager owl:equivalentClass (:manages some :Project)
:projectID rdfs:domain :Project
:Alice :manages :ProjectX
:ProjectX :projectID "123-45-6789"
All three explanations have some triples in common; but when explanations are retrieved separately, it is hard to see how these explanations are related. When explanations are merged, we get a single proof tree where alternatives for subtrees of the proof are shown inline. In indented text rendering, the merged tree for the above explanations would look as follows:
INFERRED :Alice a :Employee
ASSERTED :Manager rdfs:subClassOf :Employee
1.1) INFERRED :Alice a :Manager
ASSERTED :supervises rdfs:domain :Manager
ASSERTED :Alice :supervises :Bob
1.2) INFERRED :Alice a :Manager
ASSERTED :ProjectManager rdfs:subClassOf :Manager
INFERRED :Alice a :ProjectManager
ASSERTED :ProjectManager owl:equivalentClass (:manages some :Project)
ASSERTED :Alice :manages :ProjectX
2.1) INFERRED :ProjectX a :Project
ASSERTED :projectID rdfs:domain :Project
ASSERTED :ProjectX :projectID "123-45-6789"
2.2) INFERRED :ProjectX a :Project
ASSERTED :ResearchProject rdfs:subClassOf :Project
ASSERTED :ProjectX a :ResearchProject
In the merged proof tree, alternatives for an explanation are shown with a number id. In the above tree, :Alice a :Manager is the first inference for which we have multiple explanations so it gets the id 1. Then each alternative explanation gets an id appended to this (so explanations 1.1 and 1.2 are both alternative explanations for inference 1). We also have multiple explanations for inference :ProjectX a :Project so its alternatives get ids 2.1 and 2.2.
Special Predicates
Stardog supports some builtin predicates with special meaning in order to make queries easier to read and write. These special predicates are primarily syntactic sugar for more complex structures.
Direct/Strict Subclasses, Subproperties, & Direct Types
Besides the standard RDF(S) predicates rdf:type, rdfs:subClassOf and rdfs:subPropertyOf, Stardog supports the following special built-in predicates:
sp:directTypesp:directSubClassOfsp:strictSubClassOfsp:directSubPropertyOfsp:strictSubPropertyOf
Where the sp prefix binds to tag:stardog:api:property:. Stardog also recognizes sesame:directType, sesame:directSubClassOf, and sesame:strictSubClassOf predicates where the prefix sesame binds to http://www.openrdf.org/schema/sesame#.
We show what these each of these predicates means by relating them to an equivalent triple pattern; that is, you can just write the predicate rather than the (more unwieldy) triple pattern.
#c1 is a subclass of c2 but not equivalent to c2
:c1 sp:strictSubClassOf :c2 => :c1 rdfs:subClassOf :c2 .
FILTER NOT EXISTS {
:c1 owl:equivalentClass :c2 .
}
#c1 is a strict subclass of c2 and there is no c3 between c1 and c2 in
#the strict subclass hierarchy
:c1 sp:directSubClassOf :c2 => :c1 sp:strictSubClassOf :c2 .
FILTER NOT EXISTS {
:c1 sp:strictSubClassOf :c3 .
:c3 sp:strictSubClassOf :c2 .
}
#ind is an instance of c1 but not an instance of any strict subclass of c1
:ind sp:directType :c1 => :ind rdf:type :c1 .
FILTER NOT EXISTS {
:ind rdf:type :c2 .
:c2 sp:strictSubClassOf :c1 .
}
The predicates sp:directSubPropertyOf and sp:strictSubPropertyOf are defined analogously.
New Individuals with SWRL
Stardog also supports a special predicate that extends the expressivity of SWRL rules. According to SWRL, you can’t create new individuals (i.e., new instances of classes) in a SWRL rule.
Don’t get hung up by the tech vocabulary here…“new individual” just means that you can’t have a rule that creates a new instance of some RDF or OWL class as a result of the rule firing.
This restriction is well-motivated; without it, you can easily create rules that do not terminate, that is, never reach a fixed point. Stardog’s user-defined rules weakens this restriction in some crucial aspects, subject to the following restrictions, conditions, and warnings.
This special predicate is basically a loaded gun with which you may shoot yourselves in the foot if you aren’t very careful.
So despite the general restriction in SWRL, in Stardog we actually can create new individuals with a rule by using the function UUID() as follows:
IF {
?p a :Parent .
BIND (UUID() AS ?parent) .
}
THEN {
?parent a :Person .
}
Alternatively, we can use the predicate <http://www.w3.org/ns/sparql#UUID> as a unary SWRL built-in
This rule will create a random URI for each instance of the class :Parent and also assert that each new instance is an instance of :Person–parents are people, too!
Remarks
-
The URIs for the generated individuals are meaningless in the sense that they should not be used in further queries; that is to say, these URIs are not guaranteed by Stardog to be stable.
-
Due to normalization, rules with more than one atom in the head are broken up into several rules.
IF { ?person a :Person . BIND (UUID() AS ?parent) . } THEN { ?parent a :Parent ; a :Male . }will be normalized into two rules:
IF { ?person a :Person . BIND (UUID() AS ?parent) . } THEN { ?parent a :Parent . } IF { ?person a :Person . BIND (UUID() AS ?parent) . } THEN { ?parent a :Male . }As a consequence, instead of stating that the new individual is both an instance of
:Maleand:Parent, we would create two different new individuals and assert that one is male and the other is a parent. If you need to assert various things about the new individual, we recommend the use of extra rules or axioms. In the previous example, we can introduce a new class (:Father) and add the following rule to our schema:IF { ?person a :Father . } THEN { ?parent a :Parent ; a :Male . }And then modify the original rule accordingly:
IF { ?person a :Person . BIND (UUID() AS ?parent) . } THEN { ?parent a :Father . }
Query Rewriting
Reasoning in Stardog is based (mostly) on a query rewriting technique: Stardog rewrites the user’s query with respect to any schema or rules, and then executes the resulting expanded query (EQ) against the data in the normal way. This process is completely automated and requires no intervention from the user.
As can be seen below, the rewriting process involves five different phases.
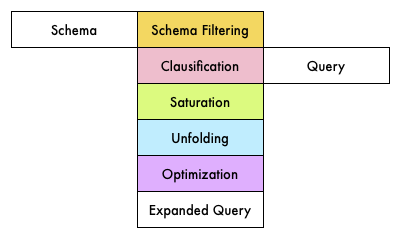
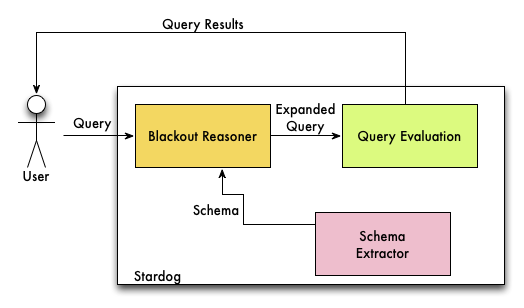
We illustrate the query answering process (the second diagram above) by means of an example. Consider a Stardog database, MyDB1, containing the following schema:
:SeniorManager rdfs:subClassOf :manages some :Manager
:manages some :Employee rdfs:subClassOf :Manager
:Manager rdfs:subClassOf :Employee
Which says that a senior manager manages at least one manager, that every person that manages an employee is a manager, and that every manager is also an employee.
Let’s also assume that MyDB1 contains the following data assertions:
:Bill rdf:type :SeniorManager
:Robert rdf:type :Manager
:Ana :manages :Lucy
:Lucy rdf:type :Employee
Finally, let’s say that we want to retrieve the set of all employees. We do this by posing the following query:
SELECT ?employee WHERE { ?employee rdf:type :Employee }
To answer this query, Stardog first rewrites it using the information in the schema. So the original query is rewritten into four queries:
SELECT ?employee WHERE { ?employee rdf:type :Employee }
SELECT ?employee WHERE { ?employee rdf:type :Manager }
SELECT ?employee WHERE { ?employee rdf:type :SeniorManager }
SELECT ?employee WHERE { ?employee :manages ?x. ?x rdf:type :Employee }
Then Stardog executes these queries over the data as if they were written that way to begin with. In fact, Stardog can’t tell that they weren’t. Reasoning in Stardog just is query answering in nearly every case.
The form of the EQ depends on the reasoning type. For OWL 2 QL, every EQ produced by Stardog is guaranteed to be expanded into a set of queries. If the reasoning type is OWL 2 RL or EL, then the EQ may (but may not) include a recursive rule. If a recursive rule is included, Stardog’s answers may be incomplete with respect to the semantics of the reasoning type.
Why Query Rewriting?
Query rewriting has several advantages over materialization. In materialization, the data gets expanded with respect to the schema, not with respect to any actual query. And it’s the data–all of the data–that gets expanded, whether any actual query subsequently requires reasoning or not. The schema is used to generate new triples, typically when data is added or removed from the system. However, materialization introduces several thorny issues:
- data freshness. Materialization has to be performed every time the data or the schema change. This is particularly unsuitable for applications where the data changes frequently.
- data size. Depending on the schema, materialization can significantly increase the size of the data, sometimes dramatically so. The cost of this data size blowup may be applied to every query in terms of increased I/O.
- OWL 2 profile reasoning. Given the fact that QL, RL, and EL are not comparable with respect to expressive power, an application that requires reasoning with more than one profile would need to maintain different corresponding materialized versions of the data.
- Resources. Depending on the size of the original data and the complexity of the schema, materialization may be computationally expensive. And truth maintenance, which materialization requires, is always computationally expensive.
Same As Reasoning
Stardog has full support for OWL 2 sameAs reasoning. However, sameAs reasoning works in a different way than the rest of the reasoning mechanism. The sameAs inferences are computed and indexed eagerly so that these materialized inferences can be used directly at query rewriting time. The sameAs index is updated automatically as the database is modified so the difference is not of much direct concern to users.
In order to use sameAs reasoning, the database configuration option reasoning.sameas should be set either at database creation time or at a later time when the database is offline. This can be done using the command line as follows:
$ stardog-admin db create -o reasoning.sameas=FULL -n myDB
There are legal three values for this option:
OFFdisables allsameAsinferences, that is, only assertedsameAstriples will be included in query results.ONcomputessameAsinferences using only assertedsameAstriples, considering the reflexivity, symmetry and transitivity of thesameAsrelation.FULLsame asONbut also considers OWL functional properties, inverse functional properties, andhasKeyaxioms while computingsameAsinferences.
The way sameAs reasoning works differs from the OWL semantics slightly in the sense that Stardog designates one canonical individual for each sameAs equivalence set and only returns the canonical individual. This avoids the combinatorial explosion in query results while providing the data integration benefits.
Let’s see an example showing how sameAs reasoning works. Consider the following database where sameAs reasoning is set to ON:
dbpedia:Elvis_Presley
dbpedia-owl:birthPlace dbpedia:Mississippi ;
owl:sameAs freebase:en.elvis_presley .
nyt:presley_elvis_per
nyt:associated_article_count 35 ;
rdfs:label "Elvis Presley" ;
owl:sameAs dbpedia:Elvis_Presley .
freebase:en.elvis_presley
freebase:common.topic.official_website <http://www.elvis.com/> .
Now consider the following query and its results:
$ stardog query execute --reasoning elvis 'SELECT * { ?s dbpedia-owl:birthPlace ?o; rdfs:label "Elvis Presley" }'
+-----------------------+---------------------+
| s | o |
+-----------------------+---------------------+
| nyt:presley_elvis_per | dbpedia:Mississippi |
+-----------------------+---------------------+
Let’s unpack this carefully. There are three things to note.
First, the query returns only one result even though there are three different URIs that denote Elvis Presley. Second, the URI returned is fixed but chosen randomly. Stardog picks one of the URIs as the canonical URI and always returns that and only that canonical URI in the results. If more sameAs triples are added the chosen canonical individual may change. Third, it is important to point out that even though only one URI is returned, the effect of sameAs reasoning is visible in the results since the rdfs:label and dbpedia-owl:birthPlace properties were asserted about different instances (i.e., different URIs).
Now, you might be inclined to write queries such as this to get all the properties for a specific URI:
SELECT * {
nyt:presley_elvis_per owl:sameAs ?elvis .
?elvis ?p ?o
}
However, this is completely unnecessary; rather, you can write the following query and get the same results since sameAs reasoning would automatically merge the results for you. Therefore, the query
SELECT * {
nyt:presley_elvis_per ?p ?o
}
would return these results:
+----------------------------------------+-----------------------+
| p | o |
+----------------------------------------+-----------------------+
| rdfs:label | "Elvis Presley" |
| dbpedia-owl:birthPlace | dbpedia:Mississippi |
| nyt:associated_article_count | 35 |
| freebase:common.topic.official_website | http://www.elvis.com/ |
| rdf:type | owl:Thing |
+----------------------------------------+-----------------------+
The URI used in the query does not need to be the same one returned in the results. Thus, the following query would return the exact same results, too:
SELECT * {
dbpedia:Elvis_Presley ?p ?o
}
The only time Stardog will return a non-canonical URI in the query results is when you explicitly query for the sameAs inferences as in this next example:
$ stardog query execute -r elvis 'SELECT * { freebase:en.elvis_presley owl:sameAs ?elvis }'
+---------------------------+
| elvis |
+---------------------------+
| dbpedia:Elvis_Presley |
| freebase:en.elvis_presley |
| nyt:presley_elvis_per |
+---------------------------+
In the FULL sameAs reasoning mode, Stardog will also take other OWL axioms into account when computing sameAs inferences. Consider the following example:
#Everyone has a unique SSN number
:hasSSN a owl:InverseFunctionalProperty , owl:DatatypeProperty .
:JohnDoe :hasSSN "123-45-6789" .
:JDoe :hasSSN "123-45-6789" .
#Nobody can work for more than one company (for the sake of the example)
:worksFor a owl:FunctionalProperty , owl:ObjectProperty ;
rdfs:domain :Employee ;
rdfs:range :Company .
:JohnDoe :worksFor :Acme .
:JDoe :worksFor :AcmeInc .
#For each company, there can only be one employee with the same employee ID
:Employee owl:hasKey (:employeeID :worksFor ).
:JohnDoe :employeeID "1234-ABC" .
:JohnD :employeeID "1234-ABC" ;
:worksFor :AcmeInc .
:JD :employeeID "5678-XYZ" ;
:worksFor :AcmeInc .
:John :employeeID "1234-ABC" ;
:worksFor :Emca .
For this database, with sameAs reasoning set to FULL, we would get the following answers:
$ stardog query execute -r acme "SELECT * {?x owl:sameAs ?y}"
+----------+----------+
| x | y |
+----------+----------+
| :JohnDoe | :JohnD |
| :JDoe | :JohnD |
| :Acme | :AcmeInc |
+----------+----------+
We can follow the chain of inferences to understand how these results were computed:
:JohnDoe owl:sameAs :JohnDcan be computed due to the fact that both have the same SSN numbers andhasSSNproperty is inverse functional.- We can infer
:Acme owl:sameAs :AcmeIncsince:JohnDoecan work for at most one company. :JohnDoe owl:sameAs :JohnDcan be inferred using theowl:hasKeydefinition since both individuals are known to work for the same company and have the same employee ID.- No more
sameAsinferences can be computed due to the key definition, since other employees either have different IDs or work for other companies.
Removing Unwanted Inferences
Sometimes reasoning can produce unintended inferences. Perhaps there are modeling errors in the schema or incorrect assertions in the data. After an unintended inference is detected, it might be hard to figure out how to fix it, because there might be multiple different reasons for the inference. The reasoning undo command can be used to see the different explanations and the reasoning undo command can be used to generate a SPARQL update query that will remove the minimum amount of triples necessary to remove the unwanted inference:
$ stardog reasoning undo myDB ":AcmeInc a :Person"
Known Issues
Stardog does not:
- Follow ontology
owl:importsstatements automatically; any imported OWL ontologies that are required must be loaded into a Stardog database in the normal way. - Handle arbitrary recursion in OWL axioms and rules. If recursion is unsupported, query results will be sound (no wrong answers) but potentially incomplete (some correct answers not returned) with respect to the requested reasoning type.
Terminology
This chapter uses the following terms:
Databases
A database (DB), a.k.a. ontology, is composed of two different parts: the schema or Terminological Box (TBox) and the data or Assertional Box (ABox). Analogus to relational databases, the TBox can be thought of as the schema, and the ABox as the data. In other words, the TBox is a set of axioms, whereas the ABox is a set of assertions.
As we explain in OWL 2 Profiles , the kinds of assertion and axiom that one might use for a particular database are determined by the fragment of OWL 2 to which you’d like to adhere. In general, you should choose the OWL 2 profile that most closely fits the data modeling needs of your application.
The most common data assertions are class and property assertions. Class assertions are used to state that a particular individual is an instance of a given class. Property assertions are used to state that two particular individuals (or an individual and a literal) are related via a given property. For example, suppose we have a DB MyDB2 that contains the following data assertions. We use the usual standard prefixes for RDF(S) and OWL.
:complexible rdf:type :Company
:complexible :maintains :Stardog
Which says that :complexible is a company, and that :complexible maintains :Stardog.
The most common schema axioms are subclass axioms. Subclass axioms are used to state that every instance of a particular class is also an instance of another class. For example, suppose that MyDB~2~ contains the following TBox axiom:
:Company rdfs:subClassOf :Organization
stating that companies are a type of organization.
Queries
When reasoning is enabled, Stardog executes SPARQL queries depending on the type of Basic Graph Patterns they contain. A BGP is said to be an “ABox BGP” if it is of one of the following forms:
- term1
rdf:typeuri - term1 uri term2
- term1
owl:differentFromterm2 - term1
owl:sameAsterm2
A BGP is said to be a TBox BGP if it is of one of the following forms:
- term1
rdfs:subClassOfterm2 - term1
owl:disjointWithterm2 - term1
owl:equivalentClassterm2 - term1
rdfs:subPropertyOfterm2 - term1
owl:equivalentPropertyterm2 - term1
owl:inverseOfterm2 - term1
owl:propertyDisjointWithterm2 - term1
rdfs:domainterm2 - term1
rdfs:rangeterm2
A BGP is said to be a Hybrid BGP if it is of one of the following forms:
- term1
rdf:type?var - term1 ?var term2
where term is either an URI or variable; uri is a URI; and ?var is a variable.
When executing a query, ABox BGPs are handled by Stardog. TBox BGPs are executed by Pellet embedded in Stardog. Hybrid BGPs by a combination of both.
Reasoning
Intuitively, reasoning with a DB means to make implicit knowledge explicit. There are two main use cases for reasoning: to infer implicit knowledge and to discover modeling errors.
With respect to the first use case, recall that MyDB2 contains the following assertion and axiom:
:stardog rdf:type :Company
:Company rdfs:subClassOf :Organization
From this DB, we can use Stardog in order to infer that :stardog is an organization:
:stardog rdf:type :Organization
Using reasoning in order to infer implicit knowledge in the context of an enterprise application can lead to simpler queries. Let us suppose, for example, that MyDB2 contains a complex class hierarchy including several types of organization (including company). Let us further suppose that our application requires to use Stardog in order to get the list of all considered organizations. If Stardog were used with reasoning, then we would need only issue the following simple query:
SELECT ?org WHERE { ?org rdf:type :Organization}
In contrast, if we were using Stardog with no reasoning, then we would have to issue a more complex query that considers all possible types of organization, thus coupling queries to domain knowledge in a tight way:
SELECT ?org WHERE
{ { ?org rdf:type :Organization } UNION
{ ?org rdf:type :Company } UNION
...
}
Which of these queries seems more loosely coupled and more resilient to change?
Stardog can also be used in order to discover modeling errors in a database. The most common modeling errors are unsatisfiable classes and inconsistent databases.
An unsatisfiable class is simply a class that cannot have any instances. Say, for example, that we added the following axioms to MyDB2:
:Company owl:disjointWith :Organization
:LLC owl:equivalentClass :Company and :Organization
stating that companies cannot be organizations and vice versa, and that an LLC is a company and an organization. The disjointness axiom causes the class :LLC to be unsatisfiable because, for the DB to be free of any logical contradiction, there can be no instances of :LLC.
Asserting (or inferring) that an unsatisfiable class has an instance, causes the DB to be inconsistent. In the particular case of MyDB2, we know that :stardog is a company and an organization; therefore, we also know that it is an instance of :LLC, and as :LLC is known to be unsatisfiable, we have that MyDB2 is inconsistent.
Using reasoning in order to discover modeling errors in the context of an enterprise application is useful in order to maintain a correct contradiction-free model of the domain. In our example, we discovered that :LLC is unsatisfiable and MyDB2 is inconsistent, which leads us to believe that there is a modeling error in our DB. In this case, it is easy to see that the problem is the disjointness axiom between :Company and :Organization.
OWL 2 Profiles
As explained in the OWL 2 Web Ontology Language Profiles Specification, an OWL 2 profile is a reduced version of OWL 2 that trades some expressive power for efficiency of reasoning. There are three OWL 2 profiles, each of which achieves efficiency differently.
- OWL 2 QL is aimed at applications that use very large volumes of instance data, and where query answering is the most important reasoning task. The expressive power of the profile is necessarily limited; however, it includes most of the main features of conceptual models such as UML class diagrams and ER diagrams.
- OWL 2 EL is particularly useful in applications employing ontologies that contain very large numbers of properties and classes. This profile captures the expressive power used by many such ontologies and is a subset of OWL 2 for which the basic reasoning problems can be performed in time that is polynomial with respect to the size of the ontology.
- OWL 2 RL is aimed at applications that require scalable reasoning without sacrificing too much expressive power. It is designed to accommodate OWL 2 applications that can trade the full expressivity of the language for efficiency, as well as RDF(S) applications that need some added expressivity.
Each profile restricts the kinds of axiom and assertion that can be used in a database. Colloquially, QL is the least expressive of the profiles, followed by RL and EL; however, strictly speaking, no profile is more expressive than any other as they provide incomparable sets of constructs. The SL profile, which is the default for Stardog, contains all three of them.