Graph Algorithms
This page discusses the details of the graph analytics algorithms. We go over the algorithms supported and the input parameters needed to run these algorithms.
Page Contents
Overview
Graph algorithms let users analyze the contents of a graph and the relationships between the nodes in a way that is not possible with SPARQL. Graph algorithms can be used for ranking nodes in a graph or detecting communities based on the connectivity of the nodes. Most of the graph algorithms work iteratively either for a fixed number of steps or until a convergence condition is met.
Graph analytics algorithms work by leveraging the Stardog Spark connector. The computation starts by submitting a Spark job that specifies the algorithm to run along with various input parameters. Spark job retrieves graph data from Stardog and runs the specified algorithm. The graph may be the complete contents of a Stardog database or a subset as defined in the input parameters. The algorithm outputs a number for each node in the input graph. The meaning of this number depends on the algorithm run and is explained below. The output numbers are then saved back to the Stardog database by connecting the node to the output value with a property.
Several input parameters apply to all algorithms whereas some input parameters are specific to some algorithms. In the following sections we describe the input parameters and the algorithms. See the Input Parameters section for how to set these parameters and the Usage for passing these parameters for execution.
General parameters
There are several parameters that are general to all analytics algorithms. These parameters are explained in the following categories based on the purpose they serve.
Connection parameters
The following parameters specify how to connect to Stardog, which database to use and the graph data that will be retrieved from that database.
The parameters in bold are required. If a value for a parameter is not provided the default value will be used.
| Parameter | Default Value | Description |
|---|---|---|
| stardog.server | N/A | Stardog server address, e.g. http://example.com:5820 |
| stardog.database | N/A | Stardog database name |
| stardog.username | admin | Username for connecting to Stardog |
| stardog.password | admin | Password for connecting to Stardog |
| stardog.query | construct { ?s ?p ?o } from <tag:stardog:api:context:local> where { ?s ?p ?o } | Query used to pull data from Stardog. The default query pulls all the data stored in the database (including the default graph and all named graphs). User can override this query with any valid CONSTRUCT query. A stored query name can be provided here instead of a query string. |
| stardog.query.timeout | N/A | Timeout that will be used for running the query. If no value is specified the timeout defined in the database settings will be used. The default timeout might need to be increased if the query pulls large amounts of data. If the timeout is set low then pulling the data would fail and Spark would retry as many times as specified in Spark settings |
| stardog.reasoning | false | Boolean flag to enable reasoning for the query. If set to true the default schema will be used for reasoning. |
| stardog.reasoning.schema | N/A | Specify a reasoning schema name for the query. If this parameter is set stardog.reasoning parameter will not have any effect and reasoning will be enabled. |
Output parameters
| Parameter | Default Value | Description |
|---|---|---|
| output.property | N/A | The Property IRI that will be used to link the node in the Stardog database to the output computed by the graph analytics algorithm. If no value is provided the property name will be auto-generated as tag:stardog:api:<AlgorithmName> based on the algorithm selected. |
| output.graph | DEFAULT | The named graph where the results will be saved to. The default graph will be used if no value is specified. |
| output.dryrun | false | The boolean flag to control if output will be written to Stardog. If set to true graph analytics algorithm will run but no information will be saved back to Stardog. Information such the number of results computed will be printed in the logs. |
Spark parameters
| Parameter | Default Value | Description |
|---|---|---|
| spark.dataset.partitions | 0 | Number of partitions that will be used to parallelize data ingestion from Stardog. Each partition corresponds to a query with a different offset, and these queries are issued in parallel. This setting does not affect the spark.sql.shuffle.partitions or spark.default.parallelism settings. Has no effect unless spark.dataset.size is specified. |
| spark.dataset.size | 0 | Total dataset size (number of triples). Needs to be calculated in advance but can be an approximate estimation. Works in combination with spark.dataset.partitions to split the data into roughly equal partitions. |
| spark.dataset.repartition | 0 | Number of partitions that will be used to parallelize the data before passing it to graph algorithm. Unlike spark.dataset.partitions, does not cause multiple queries but allows for better distribution of data across Spark worker nodes. If set to 0 (default), number of nodes in the cluster will be used. |
| spark.checkpoint.dir | stardog-graph-analytics | The checkpoint dir that will be used by the algorithms. Currently, only the Connected Components algorithm uses checkpointing. The files created in this directory will not be automatically cleaned by the Stardog connector. You can use the Spark option spark.cleaner.referenceTracking.cleanCheckpoints for automatic cleanup. |
Graph Algorithms
Page Rank
PageRank is an algorithm to measure the importance of nodes in a graph based on the quantity and quality of incoming links. The higher number of incoming links increases the importance of a node, i.e. its rank, but links from highly-ranked nodes will also have bigger effect.
The PageRank algorithm is defined recursively where the weights associated with nodes are updated at every iteration. The algorithm can be run either for a fixed number of iterations or until the values of nodes converge where no rank is being updated more than a threshold value.
Set algorithm.name=PageRank to run this algorithm. The output will be a double value representing the rank computed for each node.
The following input parameters can be specified for PageRank:
| Parameter | Default Value | Description |
|---|---|---|
| algorithm.iterations | 3 | Maximum number of iterations the algorithm will run. |
| pagerank.tolerance | N/A | The tolerance value allowed at convergence. If this option is set, PageRank algorithm will run until all the weights are smaller than this value. so setting this value smaller will yield more accurate results but will take longer to compute. |
| pagerank.reset.probability | 0.15 | Reset probability that will be used. |
Label Propagation
Label Propagation is a community detection algorithm. Each node in the graph is initially assigned to its own community. At every iteration, nodes send their community affiliation to all neighbors and update their state based on the community affiliation of incoming messages.
Label Propagation is not computationally expensive but convergence is not guaranteed. It is also possible to get trivial results where each node gets assigned to a single community.
Set algorithm.name=LabelPropagation to run this algorithm. The output will be a long value identifying the community affiliation for each node.
| Parameter | Default Value | Description |
|---|---|---|
| algorithm.iterations | 3 | Maximum number of iterations the algorithm will run. |
Strongly Connected Components
Strongly Connected Components is a kind of community detection algorithm. A strongly connected component is a set of nodes where each node is reachable from every other node by following the edges respecting the edge direction.
In the following graph, there are three strongly connected components. Nodes A, B and C form a strongly-connected component. Nodes D and E form separate singular components.
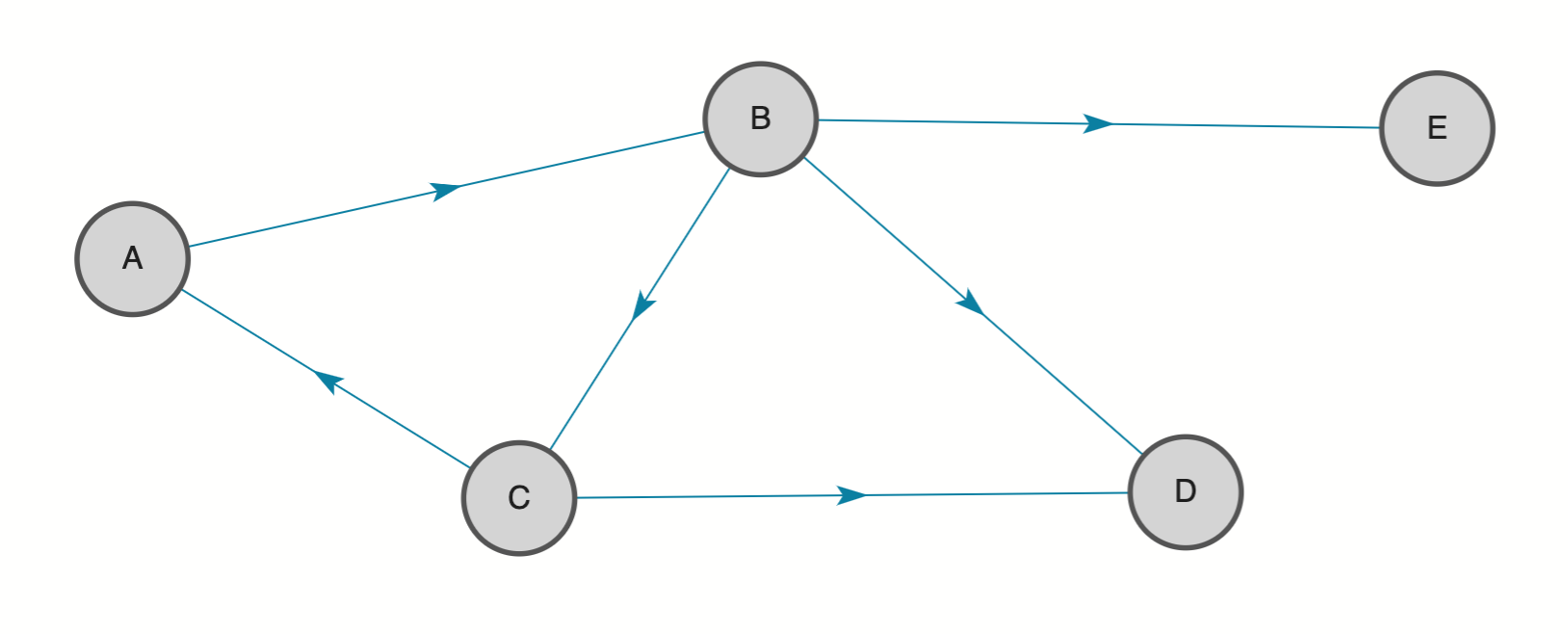
Set algorithm.name=StronglyConnectedComponents to run this algorithm. The output will be a long value identifying the component each node belongs to. The nodes with the same output value are in the same component.
| Parameter | Default Value | Description |
|---|---|---|
| algorithm.iterations | 3 | Maximum number of iterations the algorithm will run. |
Connected Components
Connected Components is a kind of community detection algorithm. A connected component is a set of nodes where each node is reachable from every other node by following the edges ignoring the edge direction.
In the following graph, there are two connected components. Node A, B and C form one connected component. Nodes D and E form another connected component.
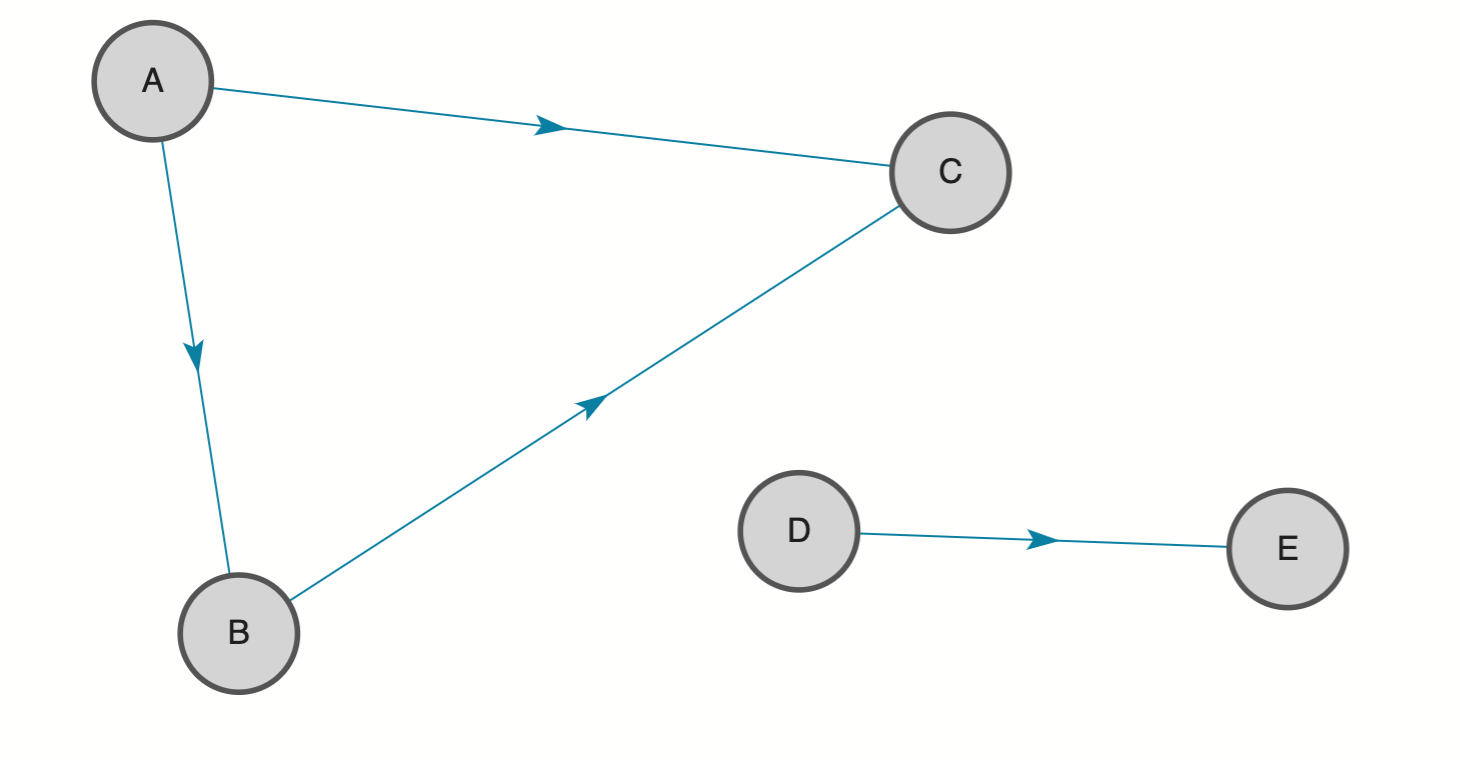
Set algorithm.name=ConnectedComponents to run this algorithm. The output will be a long value representing the component each node belongs to. The nodes with the same output value are in the same component.
| Parameter | Default Value | Description |
|---|---|---|
| algorithm.iterations | 3 | Maximum number of iterations the algorithm will run. |
Triangle Count
Triangle Count is the number of triangles a node is a member of in the graph. A triangle is defined as the three nodes connected to each other without taking the direction of the edges into account.
Set algorithm.name=TriangleCount to run this algorithm. The output will be a long value representing the number of triangles.
This algorithm has no input parameters.